sábado, 16 de enero de 2016
Ángulos entre paralelas
Ángulos externosLas parejas de ángulos: 1 y 7; 2 y 8; se llaman ángulos alternos externos, y son congruentes (figura 1)
Figuras en autocad
 Observar que las diagonales intersectan formando ángulos de 90° y a demás se cortan en el punto medio de las diagonales donde podemos observar que se forma un triangulo rectángulo , asi podemos resolver usando el teorema de pitagoras. entonces nos quedaría (r2 por que son dos radios).la forma de resolver a continuación r2+r2=3(al cuadrado)2r2=9 r= 9/2 r= 4,5 y sacamos la raíz la cual su resultado es de 2.1213
Observar que las diagonales intersectan formando ángulos de 90° y a demás se cortan en el punto medio de las diagonales donde podemos observar que se forma un triangulo rectángulo , asi podemos resolver usando el teorema de pitagoras. entonces nos quedaría (r2 por que son dos radios).la forma de resolver a continuación r2+r2=3(al cuadrado)2r2=9 r= 9/2 r= 4,5 y sacamos la raíz la cual su resultado es de 2.1213
nuestro resultado fue de 2.1213 y para sacar el área del circulo solo utilizamos la formula del área del circulo y nos da como resultado 14, 13 centímetros cuadrados y para sacar el área del cuadrado grande pues notamos que el lado mide lo mismo que el diámetro del circulo.
Un cuadrado y de área = 1600 metros cuadrados;el semicírculo de la derecha esta destinado a una alberca y las restantes áreas a juegos mecánicos y mesas con sillas para los visitantes. los limites del área verde son la alberca una diagonal del cuadrado y 1/4 de circulo determina la cantidad de pasto en rollo que se debe comparar para dicha área.
Para resolver el problema primero tenemos que sacar el área del circulo grande y dividirlo entre 8, ya que si observamos bien tomando en cuenta la diagonal se divide el circulo en 8 partes ,después tenemos que sacar el área del circulo chico y restarle el área del triangulo que se muestra en la imagen.
para sacar el are a de la parte de color simplemente tenemos que sacar el área de un circulo teniendo de dato el radio es de 20 cm . teniendo el área podemos observar que se forma un cuadrado.
entonces sacamos el área del cuadrado sabiendo que el lado mide el doble del radio y al resultado se le resta el resultado del circulo.
Propiedades de las figuras geometricas

El número de lados que tiene una figura puede ayudar a determinar qué tipo de figura geométrica es. Todas las figuras bidimensionales hechas con líneas rectas se consideran polígonos. Por ejemplo, un triángulo es una figura bidimensional que tiene tres lados. Los lados por sí solos no identifican la figura. Hay muchas figuras que tienen cuatro lados, como los cuadrados, rectángulos, rombos, trapezoides y muchas otras. Sin embargo, todas las figuras con cuatro lados se consideran cuadriláteros. Algunas figuras no tienen esquinas y por lo tanto no tienen lados distinguibles. Los círculos y los óvalos son ejemplos de figuras geométricas que no tienen lados distinguibles.
 Ángulos
Ángulos
Las figuras que tienen esquinas, también llamadas vértices, crean ángulos que pueden medirse. Los ángulos están presentes tanto en las figuras bidimensionales como en las tridimensionales. Un ángulo puede medirse usando un transportador. Un ángulo puede ser agudo, lo que significa que mide menos de 90 grados, recto, que quiere decir que es de exactamente 90 grados, u obtuso, lo que significa que es mayor a 90 grados.
Regulares e irregulares
Las figuras bidimensionales pueden clasificarse en regulares e irregulares. Los polígonos regulares son polígonos cuyos lados y ángulos interiores son congruentes, es decir, iguales. Un triángulo equilátero es un triángulo en el que los tres lados son iguales en longitud y todos los ángulos interiores son de 60 grados, lo que lo hace un triángulo regular. No todas las figuras pueden ser regulares. Un rectángulo, por ejemplo, por definición tiene dos lados que son iguales en longitud. Un lado es más largo que el otro. Esto hace que el rectángulo sea una figura irregular.
Figuras tridimensionales
 La geometría no se limita a las figuras bidimensionales. También incluye las figuras tridimensionales, llamadas también figuras sólidas. Estas figuras tienen un valor adicional de profundidad que no tienen las figuras bidimensionales. Las figuras tridimensionales se construyen con figuras bidimensionales. Por ejemplo, un cubo es una figura tridimensional que se construye con seis cuadrados ordenados en la forma de una caja. Otras figuras son una combinación de varias figuras geométricas. Un prisma es una combinación de rectángulos y triángulos.
La geometría no se limita a las figuras bidimensionales. También incluye las figuras tridimensionales, llamadas también figuras sólidas. Estas figuras tienen un valor adicional de profundidad que no tienen las figuras bidimensionales. Las figuras tridimensionales se construyen con figuras bidimensionales. Por ejemplo, un cubo es una figura tridimensional que se construye con seis cuadrados ordenados en la forma de una caja. Otras figuras son una combinación de varias figuras geométricas. Un prisma es una combinación de rectángulos y triángulos.Puntos notables de un triangulo
Puntos notables de un triangulo
incentro El incentro es el centro de la circunferencia inscrita al triángulo, por lo que la distancia a cada uno de sus lados es la misma. Más concreta mente, es el punto de intersección de las bisectrices de cada uno de los ángulos del triángulo (siendo una bisectriz la recta que divide a un ángulo en dos ángulos iguales), por lo que para representarlo gráficamente debemos dibujar las tres bisectrices y localizar el punto de intersección de las mismas.
incentro El incentro es el centro de la circunferencia inscrita al triángulo, por lo que la distancia a cada uno de sus lados es la misma. Más concreta mente, es el punto de intersección de las bisectrices de cada uno de los ángulos del triángulo (siendo una bisectriz la recta que divide a un ángulo en dos ángulos iguales), por lo que para representarlo gráficamente debemos dibujar las tres bisectrices y localizar el punto de intersección de las mismas.
El baricentro (también llamado centroide) de un triángulo es el punto de intersección de las medianas de dicho triángulo (siendo una mediana el segmento que une un vértice con el punto medio del lado opuesto). Por ello, para representar gráficamente el baricentro debemos dibujar las tres medianas y localizar el punto en el que se corta.
lunes, 11 de enero de 2016
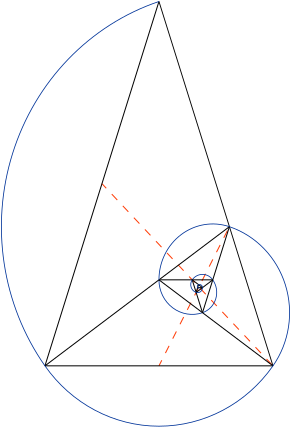
ARGUMENTOS RECTÁNGULO ÁUREO
Este número es que
en la naturaleza si representa armonía, o al menos considero
que guarda un secreto y misterio, y me sorprende la manera en que este se
representa y se relaciona con esta misma. Aunque también
pienso que el hombre solo ha buscado objetos para relacionarlos sea como sea
con esta proporción.
Se dice que se
encuentra en todas partes, sin embargo creo el hombre lo ha utilizado para
embellecer sus obras a partir de que Luca Pacioli lo definió como la Divina
proporción.
El numero aureo ha
tomado cierta moda en los últimos años debido a lo que se dice de el, ya que
se considera un numero que representa divinidad. Nuestros antepasados conocían
este número y lo utilizaban, ya que su presencia introduce una proporción,
estéticamente hablando, muy agradable.
Este número hace referencia a un número de propiedades un tanto especiales, que
aparece de un modo u otro en infinidad de obras artísticas y también en la
Naturaleza, tanto en nuestro mundo como en el cielo.
La idea es la
siguiente: El todo se divide en dos partes tal que, la razón proporcional
entre la parte menor y la mayor, es igual a la existente entre la mayor y el
total, es decir, la suma de ambas.
Leonardo de Pisa
(1170-1250), más conocido como Fibonacci, nació en Pisa, Italia e hizo muchas
contribuciones a las matemáticas. Es conocido por todo el mundo por la
secuencia de números que lleva su nombre: {0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55,
89, 144, 233, 377, 610, 987, 1597, ...}. Esta secuencia se construye mediante
la elección de los dos primeros números y el número siguiente se obtiene como
la suma de los dos números anteriores.
La secuencia
formada a partir de la relación entre los números adyacentes de la secuencia de
Fibonacci converge a un valor constante de 1,6180339887..., llamado
"phi", cuyo símbolo es Φ.
Este es un
rectángulo muy especial, ya que los griegos lo consideraban de particular
belleza y lo utilizaron frecuentemente en su arquitectura. Al parecer a la
mayoría de las personas también les parece más agradable a la vista un
rectángulo con esas proporciones entre sus lados y les parece “atractivo” y
hasta “armonioso”.
Estos rectángulos
son la base para generar una curva conocida como la "espiral dorada",
una espiral logarítmica que se ajusta bastante bien a otras espirales que se
encuentran en la naturaleza. Este hecho es la fuente de gran parte del interés
popular y mística en este asunto matemático.
La "espiral
de oro" es una curva fascinante. Pero es sólo un miembro más de una
familia más grande de curvas espirales, conocidas colectivamente como espirales
logarítmicas, y todavía hay muchas otras espirales que se encuentran en la
naturaleza, como la espiral de Arquímedes.
 Inconsciente o
conscientemente se diseñan infinidad de cosas y artículos que resultan
tener la forma de un rectángulo áureo: vajillas, cuatros, fotografías,
construcciones e incluso hasta tatuajes. Científicamente no es posible
confirmar si es verdad que este rectángulo cause en nosotros un efecto para que
podamos considerar “bellas” ciertas cosas.
Inconsciente o
conscientemente se diseñan infinidad de cosas y artículos que resultan
tener la forma de un rectángulo áureo: vajillas, cuatros, fotografías,
construcciones e incluso hasta tatuajes. Científicamente no es posible
confirmar si es verdad que este rectángulo cause en nosotros un efecto para que
podamos considerar “bellas” ciertas cosas.
Se dice que tal
vez lo anterior se deba a que encontramos el rectángulo áureo en diversas
partes de la naturaleza. Lo podemos ver en caracolas, galaxias, células,
plantas, en el cuerpo humano y en muchos ejemplos más relacionados con la
creación de la naturaleza. También se percibe como el número de la belleza y la
armonía, ya que ha sido empleado en las obras más espectaculares realizadas por
la humanidad, desde las pirámides hasta cuadros, murales, catedrales o en la
música.
En mi opinión, el
que el rectángulo áureo parezca causar “armonía” y que todos los objetos
diseñados por ese principio sean “bellos”, me parece muy subjetivo. Según los
filósofos Griegos y Romanos, el secreto de la belleza se esconde en la simetría
y en una proporción "perfecta" que siguen los seres vivos y que
provoca que resulten bellos y estéticamente atractivos. Pero para mí la belleza
es subjetiva, lo que causa que cada quién pueda percibir diferentes cosas y
tener distintas opiniones sobre si algo es carente o no de belleza. ¿En qué me
baso para decir esto?, para empezar hay que definir que es belleza. La belleza
está asociada a la hermosura. Se trata de una apreciación subjetiva: lo que es
bello para una persona, puede no serlo para otra. Una persona puede ver alguna
fotografía basada en la razón de oro e inconscientemente pensar que es bella y
gustarle y simplemente otra puede pensar que es una simple fotografía sin nada
especial.
Pero como ahora
desde que fue descubierto y difundido el rectángulo áureo y sus “efectos”, se
ha comercializado en gran medida por muchos lados y por las más grandes
compañías del mundo, con el fin de que sus logos “atraigan” a más personas a
consumir sus productos. Esto ha causado que la mayoría de las personas se
sugestionen a tal punto que creen que todo lo que ven en relación a esta razón,
es armonioso o bello.
Apple es una de
las pocas empresas que no usa el nombre de la compañía en su logo. Sin embargo,
el logo de Apple es uno de los más reconocidos símbolos en el mundo. El logo se
dice está perfectamente balanceado, y las líneas que trazan el logo son
círculos con diámetros proporcionales a la serie de Fibonacci. Y si Apple es
una marca muy conocida, pienso que es por la calidad de sus productos y la
versatilidad de los mismos. Si causara armonía en nosotros, la mayoría de las
personas tendríamos uno sin importar el costo, simplemente por el efecto que
causaría. Sin embargo, utilizamos tecnología de otras marcas.
Existe un video en
internet llamado “Las proporciones de la belleza”, en el cual se relata cuáles
son las medidas que debe tener un rostro para que pueda ser considerado como
“bello”. Por medio de la razón de oro se construye una máscara con ciertas
proporciones, que colocada sobre algunas fotografías de famosos
estadounidenses, se determina si es atractivo. Uno de los resultados que arrojó
este experimento es que Tom Cruise, encaja perfectamente en esta máscara de
“perfección”, pero como mencione un poco más arriba en este ensayo, la belleza
es subjetiva. Pregunte a tres personas si les parecía atractivo y solamente dos
me contestaron que sí, por lo parece que lo que es establecido “bello” o
“atractivo” solo lo es para algunas personas.
En la naturaleza
se afirma que podemos ver el rectángulo áureo en la concha de los caracoles,
pero tiene esa forma porque simplemente es así crecimiento. A medida que el
nautilo crece, el extremo abierto de su caparazón aumenta de diámetro a una
velocidad casi constante. Está forzado a curvarse alrededor del caparazón
existente.
No es difícil
encontrar que una de estas curvas que se trazan en el rectángulo áureo se
ajusta a algún objeto particular en la naturaleza. Sin embargo, cuando una
forma parece encajar, rara vez ese ajuste es exacto. Los ejemplos de la
naturaleza que se encuentran en los libros e incluso en internet, suelen tener
variaciones considerables del "ideal áureo". A veces, las curvas que
dicen coincidir con la espiral dorada, se ajustan mejor, en realidad, por
alguna otra espiral que se le añade. Un ejemplo claro de ello es el caparazón
del nautilus.
Otro ejemplo muy
famoso es que la proporción de oro tiene que ver los las flores de girasol. Las
semillas en el girasol es un ejemplo de la observación que el botánico William
Hofmeister hizo en 1868: los primordios (parte de la flor de se forman preferentemente
donde haya mayor espacio disponible para ellos. También se deben formar donde
queden unidos de manera eficiente al resto de la planta, y esta es la
consideración geométrica. El patrón también puede ser modificado por la humedad
y los nutrientes, que afectan el tamaño de las semillas en formación. El patrón
rara vez sale perfectamente adaptado a la proporción áurea. Sólo las veces que
se aproxima, son las que se van a ser fotografiados para los artículos sobre
los números de Fibonacci.
Otro ejemplo del
que se habla en donde también podemos observar la razón aurea en la cola de un
pavorreal. Las manchas en las plumas de su cola parecen formar patrones en
espiral. ¿Son éstas espirales doradas o corresponden a algún otro tipo de
espiral? La ecuación matemática exacta de la espiral depende de cuán lejos el
pájaro decida desplegar su cola. Lo cual nos indica que no siempre podremos
apreciar que se forman espirales relacionados con la razón áurea.
No es muy difícil
encontrar ejemplos para casi cualquier patrón o relación matemática que se
desee. Por eso, algunas personas cometen el error de suponer que esto revela un
principio que rige la naturaleza y como esta va a ser.
Como mencione al
inicio de mi ensayo, los griegos utilizaban este rectángulo en muchas de sus
construcciones, ya que lo consideraban algo especial. No fue de esperarse que
esto inspirará a grandes escultores y pintores de la antigüedad y hayan
adoptado esta proporción como modelo de armonía y de belleza.
Artistas y
matemáticos como Lucca Pacioli, Leonardo Da Vinci o como Alberto Durero
designaron a este número con nombres tan expresivos como sección áureo, razón
áurea o divina proporción. Desde el Renacimiento, muchos pintores han utilizado
en sus obras maestras con dimensiones relacionadas con la razón áurea.
Leonardo Da Vinci
fue pintor, anatomista, arquitecto, paleontólogo, artista, botánico,
científico, escritor, escultor, filósofo, ingeniero, inventor, músico, poeta y
urbanista.
Da Vinci tenía la
idea de que las formas de la naturaleza, incluyendo las especies animales,
contenían la justa proporción de la belleza. Para Leonardo, la belleza era el
efecto visual de proporciones armoniosas.
En muchas obras Da
Vinci, representó la belleza de la proporción áurea sobre el cuerpo humano. Unas
proporciones armoniosas para el cuerpo, que estudiaron antes los griegos y
romanos, las plasmó en el “Hombre de Vitruvio”. Sirvió para ilustrar el libro
“La Divina Proporción” de Luca Pacioli. Resulta que el cociente entre la altura
del hombre (lado del cuadrado) y la distancia del ombligo a la punta de la mano
(radio de la circunferencia) es el número áureo.
Leonardo da Vinci
realiza una visión del hombre como centro del Universo al quedar plasmado en un
círculo y un cuadrado. En él se realiza un estudio anatómico buscando la
proporcionalidad del cuerpo humano: el ideal de belleza. También Da Vinci
utilizó esta razón para pintar su tan famosa pintura “La Mona Lisa”.
 Alberto Durero,
aprovechó la “armonía” y “belleza” que desprende del número áureo en la composición
de muchas obras, para representar a Adán y Eva.
Alberto Durero,
aprovechó la “armonía” y “belleza” que desprende del número áureo en la composición
de muchas obras, para representar a Adán y Eva.
Vincent Van Gogh
percibió en los últimos momentos de su vida, la presencia obsesiva de estas
espirales de áurea en toda la naturaleza, y las ilustró en el cielo de su
famoso cuadro “La Noche estrellada”, y en su famoso Autorretrato de mirada
penetrante y enloquecida. Los torbellinos espirales aparecen en la mayoría de
sus obras durante su último días en el manicomio de Saint-Rémy, el último año
antes de su suicidio. Se dice que Gogh había descubierto el secreto de la
naturaleza para crear la belleza.
Todos los
personajes anteriormente mencionados se tratan de pintores que han sido
reconocidos por sus grandes y magnificas obras de arte realizadas, pero como
todas las cosas en el mundo el arte es uno de los temas más subjetivos. Hay
quienes les gusta el arte de un determinado pintor, pero al igual habrá gente
que no le guste su obra.
Principalmente se
conocen las obras y se hacen famosas, por la historia que hay detrás de ellas.
Por ejemplo, las pinturas de Da Vinci se caracterizan por ser pinturas repletas
de “misterio”. Se decía que él dejaba en todas sus pinturas algún mensaje o
imagen oculta, además de que eran reconocidas sus obras por la técnica de
pintura y el material utilizado.
¿Quién no conoce a
Vincent Van Gogh?, el artista que se cortó una oreja y cuyas obras de arte son
realmente interesantes.
Muy a pesar de que
han pasado muchísimos años desde que fue descubierto el rectángulo áureo y su
relación con la armonía y en la belleza, hay quienes en la actualidad (muy por
aparte de los logos de las compañías) las utilizan para llevar a cabo su
trabajo.
Si miramos a
nuestro alrededor hay muchos ejemplos, en arquitectura, en el diseño o la
fotografía.
La arquitectura
contemporánea sigue utilizando la proporción aurea en diferentes estructuras.
En los años 40s se desarrolló un sistema de proporciones llamado Modulor en el
que la proporción de alturas estaba basada en la proporción aurea.
 En la arquitectura
la proporción aurea encuentra variadas e imaginativas aplicaciones, como
el caso del círculo áureo, círculo dividido en dos secciones por dos
radios, en el cual el cociente de la división del ángulo mayor entre el menor
es igual al número de oro.
En la arquitectura
la proporción aurea encuentra variadas e imaginativas aplicaciones, como
el caso del círculo áureo, círculo dividido en dos secciones por dos
radios, en el cual el cociente de la división del ángulo mayor entre el menor
es igual al número de oro.
La proporción
aurea en la actualidad es utilizada en las fachadas para la asignación de
tamaños proporcionales en ventanas, puertas, columnas, lozas, arcos, trabes,
elementos decorativos, de tal forma que se logre un conjunto visualmente
“atractivo” y se mantenga la proporcionalidad con respecto a la fachada
total.
Un ejemplo del uso
de la proporción áurea contemporánea es La Casa de la Moneda China, en Santa
Cruz de la Sierra, Bolivia. Cuyo autor es Juan Carlos Menacho Durán, tanto los
radios de las circunferencias como las medidas de los rectángulos, reflejan la
proporción áurea.
También, los
inversionistas a menudo buscan el "santo grial", un método matemático
para predecir el mercado de valores y algunos analistas del mercado de valores
utilizan la serie de Fibonacci para orientar sus inversiones.
E incluso otro
ejemplo actual en el cual se encuentra el rectángulo áureo, es en las tarjetas
de crédito.
Hay quienes
concuerdan en que el rectángulo áureo y su supuesta relación que tiene con la
“belleza” y la “armonía” es falso, se trata del libro “Misconceptions about the
Golden ratio” de George Markowsky.
 Los números de
Fibonacci y la proporción áurea han sido motivo de todo tipo de especulaciones
sobre su supuesta presencia en distintas manifestaciones de la naturaleza y en
otras hechas por el hombre. Así se suele afirmar que se puede encontrar la
proporción dorada en lugares tales como el número de pétalos de las flores y en
las hojas de las plantas, en las caparazones de moluscos, en la forma de
ciertas galaxias, en obras de arte e inclusive en el tamaño de las tarjetas de
crédito. Pero desde mi punto de vista es un tema que se trata en un 100% de
subjetividad.
Los números de
Fibonacci y la proporción áurea han sido motivo de todo tipo de especulaciones
sobre su supuesta presencia en distintas manifestaciones de la naturaleza y en
otras hechas por el hombre. Así se suele afirmar que se puede encontrar la
proporción dorada en lugares tales como el número de pétalos de las flores y en
las hojas de las plantas, en las caparazones de moluscos, en la forma de
ciertas galaxias, en obras de arte e inclusive en el tamaño de las tarjetas de
crédito. Pero desde mi punto de vista es un tema que se trata en un 100% de
subjetividad.
Finalmente quiero
terminar con la siguiente cita: “Ciertamente, la afirmación frecuentemente
repetida de que el Partenón de Atenas está basado en la proporción áurea no es
compatible con las mediciones reales. De hecho, toda la historia de los griegos
y la razón de oro parece algo sin fundamento. Lo único que sabemos con certeza
es que Euclides en su famoso libro de texto (escrito alrededor del 300ac)
Elementos, muestra cómo calcular su valor”
Keith Devlin.
Matemático.
sábado, 9 de enero de 2016
Razón áurea en el arte.
Razón áurea en el arte.
La espiral dorada (denominada también espiral de áurea) es una espiral logarítmica asociada a las propiedades geométricas del rectángulo dorado. La razón de crecimiento es Φ, la naturaleza (plantas, galaxias, espirales), así como en el arte. La proporción áurea se
basa en una medida o número llamado también áureo, de oro, y representado por
la letra griega φ (fi) (en minúscula) o Φ (fi) (en mayúscula). Es una
proporción de más o menos: 2 + 1,6 , es decir, que una medida a=2 más
otra medida b=1,618…. forman una medida que sumaría c= 3,618…. que existe esta proporción áurea entre unas medidas a, b y c. Y que, por lo tanto, tienen este equilibrio
mágico donde una medida contiene a otra más un poquito extra. 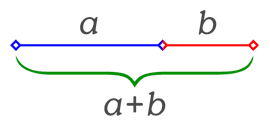
Para
que un segmento sea particionado en sección áurea la razón entre el segmento y la parte mayor debe ser igual a la razón entre la parte mayor y la menor.
Rectángulo ÁureoTodo se divide en dos partes tal que, la razón proporcional entre la
parte menor y la mayor, es igual a la existente entre la mayor y el total, es
decir, la suma de ambas.
Traza un cuadrado ABCD de cualquier medida.se localiza el punto medio M de la base AB. Utiliza el compas con una abertura igual a la distancia desde el punto M hasta uno de los vértices, ya sea C o D.Desde el punto C trazar un circulo con centro en el punto M, que este sera el punto P. Con abertura de AP y centro en el punto D trazar un arco. Donde intersectan los puntos, llamado punto Q, sera la unión del punto P y Q
Suscribirse a:
Comentarios (Atom)